Mechanical Properties of Solids Detailed notes for the prep of JEE/NEET. This note is the best for your competitive exam preparation like JEE.NEET.
Table of Contents
MECHANICAL PROPERTIES OF SOLIDS Detailed Notes for JEE/NEET
INTERATOMIC AND INTERMOLECULAR FORCE
The force between atoms of an element is called interatomic force. The force between molecules of a compound (or element) is called intermolecular force. These forces are electrical in nature. Depending on the distance between the atoms, this force may be attractive or repulsive in nature. These forces are responsible for the definite size or shape of a solid.
Detailed calculations as well as deductions from experiment show that the interaction between any isolated pairs of atoms or molecules may be represented by a curve that shows how the potential energy varies with separation between them as shown in the figure.
This curve describes the interatomic potential. The force between the atoms can be found from the potential energy by using the relation
The resulting interatomic force curve is shown in figure. Force is along the line joining the atoms or molecules, and is shown negative for attraction and positive for repulsion.
We see that as the distance decreases, the attractive force first increases and then decreases to zero at a separation where the potential energy is minimum.
For smaller distance force is repulsive, because at these distance the negative charge distribution associated with one atom begins to overlap with that associated with the neighbouring atom.
The negative sign shows that Fa is a force of attraction and ‘a’ is a constant which depends on the kind of attractive force between the molecules and the structure of the molecules. The force of attraction results from the creation of induced dipole moment in one molecule by the neighbouring molecule.
When the molecules are brought closer there is a force of repulsion between them. It can be shown that the repulsive force is,
where b is a constant like a. The force of repulsion varies very rapidly. Fr is inversely proportional to the ninth power of distance between the molecules.
The resultant force acting on the molecules is
The distance between the molecules decides the sign of the resultant force.
ELASTICITY
The property of the body by virtue of which it tends to regain its original shape and size after removing the deforming force is called elasticity. If the body regains its original shape and size completely, after the removal of deforming forces, then the body is said to be perfectly elastic.
PLASTICITY
The property of the body by virtue of which it tends to retain its deformed state after removing the deforming force is called plasticity. If the body does not have any tendency to recover its original shape and size, it is called perfectly plastic.
STRESS AND STRAIN
STRESS
When a deforming force is applied to a body, an internal restoring force comes into play.The restoring force per unit area is called stress.
Its S.I. Unit is Nm-2Stress is a tensor as its value changes when direction changes.TYPES OF STRESS
- Longitudinal stress or Tensile stress
- Volumetric stress
- Tangential stress
STRAIN
It is defined as the ratio of the change in shape or size to the original shape or size of the body.
Strain has no units or dimensions.
TYPES OF STRAIN
- Longitudinal strain : It is defined as the ratio of the change in length to the original length.
Longitudinal strain =
- Volume strain : It is the ratio of the change in volume to the original volume.
Volume strain =
- Shearing strain : It is the angular deformation produced in a body.
Shearing strain (θ) =
HOOKE’S LAW
It is the fundamental law of elasticity given by Robert Hooke in 1679. It states that “the stress is directly proportional to strain provided the strain is small “. i.e. Stress ∝ strain This proportionality constant is called modulus of elasticity (name given by Thomas Young) or coefficient of elasticity (E).Since stress has same dimensions as that of pressure and strain is dimensionless. So the dimensions of E is same as, that of stress or pressure i.e. [ML–1T–2]
The modulus of elasticity depends on the material and on the nature of deformation. There are three type of deformations and therefore three types of modulus of elasticity.
- Young’s modulus (Y) : It measures the resistance of a solid to elongation.
- Shear modulus or modulus of rigidity (η) : It measures the resistance to motion of the plane of a solid sliding part on each other.
- Bulk modulus (B) : It measure the resistance that solid or liquid offer to their volume change.
The stress under which the system breaks is called breaking stress.
YOUNG’S MODULUS (Y)
Let us consider a long bar (shown in fig.) of cross-sectional area A and length lo, which is clamped at one end. When we apply external force Fl longitudinally along the bar, internal forces in bar resist distortion, but bar attains equilibrium in which its length is greater and in which external force is exactly balanced by internal forces. The bar is said to be stressed in this condition.
Now if the solid bar obey the Hooke’ law, the Young’s modulus, Y is defined as
Where Δl is change in the length of bar, when we apply Fl.
SHEAR MODULUS (η)
Shear modulus or modulus of rigidity η is
- As we see, there is no change in volume under this deformation, but shape changes.
- (see the figure), where θ is shear angle.
BULK MODULUS (B)
The Bulk modulus B is defined as
Negative sign comes to make B positive, because with the increase of pressure, the volume of body decreases or vice versa. The reciprocal of the Bulk modulus is called compressibility of material i.e., Compressibility = 1/B
POISSON’S RATIO (σ)
Lateral strain/longitudinal strain = Poisson’s ratio (σ)The theoretical value of σ lies between –1 and 0.5 and practical value of σ lies between 0 and 0.5.
STRESS-STRAIN CURVE
- Proportional limit : The limit in which Hooke’s law is valid i.e, stress is directly proportional to strain is called proportion limit. Stress ∝ strain
- Elastic limit : It is a maximum stress upto which the body completely recovers its original state after the removal of the deforming forces.
- Yield point : The point beyond elastic limit, at which the length of wire starts increasing without increasing stress, is defined as the yield point.
- Breaking point : The position when the strain becomes so large that the wire breaks down at last, is called breaking point. At this position the stress acting in that wire is called breaking stress and strain is called breaking strain.
- Breaking stress is also known as the tensile strength.
- Metals with small plastic deformation are called brittle.
- Metals with large plastic deformation are called ductile.
ELASTIC FATIGUE
This is the phenomenon of a delay in recovering the original configuration by a body, if it had been subjected to stress for a longer time the body loses the property of elasticity temporarily.
ELASTIC RELAXATION TIME
It is the time delay in regaining the original shape after removal of deforming forces. Elastic relaxation time for gold, silver and phosphor bronze is negligible.
ELASTIC HYSTERESIS
When the stress applied on a body, is decreased to zero, the strain will not be reduced to zero immediately. For some substances (e.g.-vulcanized rubber), the strain lags behind the stress. This lagging of strain behind stress is called elastic hysteresis.
The stress-strain graph for increasing and decreasing load encloses a loop, as shown in figure. The area of the loop gives the energy dissipated during its deformation.
KEEP IN MEMORY
- Thermal stress ,where α is the coefficient of linear expansion and ΔT is the change in temperature.
- The modulus of rigidity (η) for liquids is zero.
- For a given tensile force, the increase in length is inversely proportional to square of its diameter.
- The pressure required to stop volume expansion of a piece of metal is P=BγdT, where γ = coefficient of volume expansion = 3α
- To compare elasticities of different materials, their identical small balls are made and they are dropped from same height on a hard floor. The ball which rises maximum after striking the floor, is most elastic. The order of elasticity of different materials on this basis is as follows : Yivory > Ysteel > Yrubber > Yclay
- For the construction of rails, bridges, girders and machines, materials with high Young’s modulus are used so that they may not get permanently deformed.
For a spring, F = Hence spring constant k = . Here ΔL = x.
- When equal force is applied on identical wires of different materials then the wire in which minimum elongation is produced is more elastic. For the same load, more elongation is produced in rubber than in steel wire, hence steel is more elastic than rubber.
Relation between Y, B, η and σ
- Y = 3B(1 – 2σ)
- Y = 2η (1 + σ)

Torsional rigidity of a cylinder
- The torsional rigidity C of a cylinder is given by,
where = modulus of rigidity of material of cylinder, R = radius of cylinder, l = length of cylinder
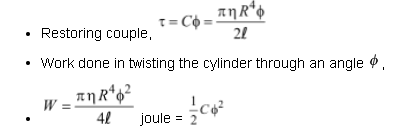
CANTILEVER
A beam fixed at one end and loaded at the other end is called a cantilever.
- The depression y at a distance x from the fixed end is (when the weight of cantilever is ineffective)
where mg = load applied, l = length of cantilever,
I = geometrical moment of inertia of its cross section.

KEEP IN MEMORY
- Wound spring possess elastic potential energy.
- A material which can be drawn into wires is called ductile and a material which can be hammered into sheet is called malleable.
- Ductility, brittleness, malleability, etc., are not elastic properties.
- The substance which breaks just beyond the elastic limit is called brittle.
- (i) Breaking force of a wire = breaking stress × area of cross section
(ii) Breaking stress does not depend on the length of wire(iii) Breaking stress depends on the material of wire.

